La Distribution de Poisson : Plus Qu’un Simple Poisson d’Avril Statistique
Ah, la distribution de Poisson ! Non, non, pas le poisson que vous mangez, mais plutôt le concept statistique qui décrit la fréquence des événements dans un intervalle de temps ou d’espace donné. C’est un outil fascinant, et étonnamment utile, même si son nom peut prêter à confusion, surtout en français où « poisson » évoque immédiatement… eh bien, un poisson. Accrochons-nous et plongeons dans le vif du sujet, sans arêtes, promis.
I. Les Fondamentaux de la Distribution de Poisson : Plus Que de Simples Chiffres
La distribution de Poisson est votre alliée pour analyser des données de comptage. Imaginez que vous comptez des choses : le nombre de clients qui franchissent la porte d’un magasin en une heure, le nombre de défauts dans une série de produits, ou encore le nombre d’accidents de la route à un carrefour précis chaque jour. Ce sont tous des exemples parfaits où la distribution de Poisson entre en jeu.
Pour que ça fonctionne, il y a quelques règles du jeu à respecter. Les événements que vous comptez doivent être indépendants les uns des autres. L’arrivée d’un client ne doit pas influencer l’arrivée du prochain, par exemple. Et ils doivent se produire à un rythme constant. Pas de panique si ça semble abstrait, les exemples concrets vont éclaircir tout ça :
- Le nombre de clients qui arrivent dans un magasin en une heure.
- Le nombre de défauts trouvés dans un produit manufacturé.
- Le nombre d’accidents de la circulation à une intersection par jour.
- Le nombre de courriels que vous recevez quotidiennement (surtout les spams, malheureusement).
- Le nombre de visiteurs sur un site web par heure (les robots comptent aussi!).
Distribution de Poisson vs. Distribution Binomiale : Le Duel des Distributions
On mélange souvent Poisson et Binomiale, mais elles ont leurs propres terrains de jeu. La distribution binomiale est là quand vous avez un nombre fixe d’essais (disons, vous lancez une pièce 10 fois) et une probabilité constante de succès à chaque essai (la probabilité de tomber sur pile est toujours de 0.5, en théorie).
La distribution de Poisson, elle, préfère les situations avec une taille d’échantillon variable et un taux moyen d’occurrence constant. Pensez au nombre de voitures qui passent un péage en 5 minutes, puis en 10 minutes, puis en 1 heure. Le temps varie, mais le taux moyen de passage reste (plus ou moins) le même.
Astuce de pro : Quand vous avez un grand nombre d’essais (n) et une faible probabilité de succès (p), la distribution de Poisson peut même approximer la binomiale. C’est un peu comme utiliser un marteau pour planter un clou… ça fonctionne, mais ce n’est peut-être pas l’outil le plus précis.
Un détail crucial : la moyenne et la variance d’une variable aléatoire de Poisson sont toujours égales. C’est une caractéristique qui peut vous aider à l’identifier rapidement. Et oui, c’est une probabilité discrète, on parle d’événements qu’on peut compter, pas mesurer en continu. L’intervalle de temps est fixe, et la fameuse valeur lambda (λ), qui représente le taux moyen d’événements, est toujours supérieure à zéro. Et pour finir, le processus de Poisson est sans mémoire. Le passé n’influence pas le futur, chaque événement est un nouveau départ.
II. Le Processus de Poisson : Le Temps Qui S’écoule, Les Événements Qui Arrivent
Le processus de Poisson, c’est le modèle mathématique qui décrit l’arrivée d’événements dans le temps, avec ce fameux taux moyen fixe (λ). Imaginez une rivière qui coule à débit constant, les événements sont comme des gouttes d’eau qui tombent à un rythme régulier.
Quelques conditions définissent ce processus :
- N(0) = 0 : Au temps zéro, aucun événement n’a encore eu lieu. Logique, non ?
- N(t) a des incréments indépendants : Le nombre d’événements dans un intervalle de temps n’influence pas le nombre d’événements dans un autre intervalle disjoint.
- Le nombre d’arrivées dans un intervalle de temps τ > 0 suit une distribution de Poisson de paramètre (λτ) : C’est un peu technique, mais ça signifie simplement que la distribution de Poisson est au cœur du processus.
Les exemples concrets sont légion :
- L’arrivée de clients dans un magasin (encore eux!).
- Le nombre de défauts dans un processus de fabrication (toujours ennuyeux, mais statistiquement intéressants).
- Le nombre d’appels reçus par un centre d’appels (surtout aux heures de pointe!).
- Le nombre d’accidents à une intersection donnée (espérons le moins possible!).
- Le nombre de courriels reçus par une personne (la boîte de réception déborde!).
Un domaine d’application privilégié ? La théorie des files d’attente. Comprendre et modéliser les files d’attente, que ce soit à la caisse du supermarché ou sur un serveur informatique, c’est crucial, et la distribution de Poisson est souvent au centre de l’équation.
III. La Régression de Poisson : Prédire la Fréquence des Événements
La régression de Poisson, c’est l’étape suivante. On ne se contente plus de décrire, on veut prédire. L’objectif ? Analyser des données de comptage pour comprendre quels facteurs influencent la fréquence d’un événement.
L’interprétation des coefficients de régression est un peu particulière. Pour chaque unité d’augmentation d’une variable prédictive, la différence des logarithmes des comptages attendus change du coefficient de régression correspondant, en gardant les autres variables constantes. Dit plus simplement, ça nous indique comment la fréquence de l’événement varie en fonction de chaque facteur, toutes choses égales par ailleurs. C’est subtil, mais puissant.
En pratique, on utilise la régression de Poisson pour modéliser le nombre de cas de maladies ou d’hospitalisations en fonction de l’âge, du sexe, des conditions environnementales… Des questions de santé publique cruciales, abordées avec les outils statistiques appropriés.
IV. Poisson Face aux Autres Distributions : Un Match Statistique
Revenons sur les comparaisons, car c’est souvent là que les choses se clarifient. Poisson vs. Binomiale, on a déjà vu : nombre d’essais fixe vs. variable. Mais Poisson vs. Normale, alors ?
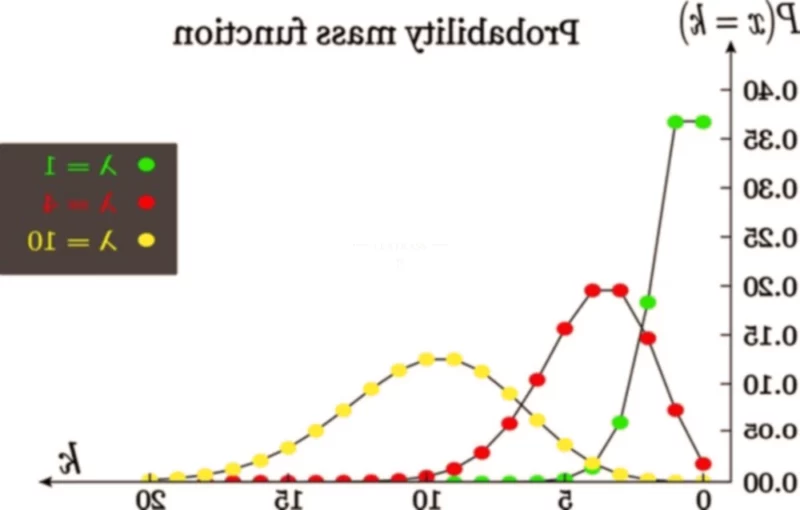
La distribution normale, c’est la cloche, toujours symétrique. La distribution de Poisson, elle, est plus versatile. Sa forme change en fonction de sa moyenne. Avec une moyenne faible, elle est très asymétrique, avec le mode à zéro. Plus la moyenne augmente, plus elle tend vers la symétrie, et peut même ressembler à une normale. Mais attention, ce n’est jamais tout à fait la même chose.
V. Les Propriétés Mathématiques : La Formule Magique
La formule de la distribution de Poisson ? Elle décrit la probabilité d’obtenir un nombre entier non négatif d’événements. C’est une formule, certes, mais elle est là pour nous simplifier la vie, pas la compliquer. Le cœur de cette formule, c’est lambda (λ), qui, je le répète, est la moyenne de la distribution. Et puis il y a e, la constante mathématique, environ 2.71828. Un nombre fascinant, qui se cache un peu partout en mathématiques, et même dans la distribution de Poisson.
VI. « Poisson » en Français : Plus Qu’une Simple Statistique, Un Mot Plein de Sens
Parlons un peu de la langue française. « Poisson », vous le savez, c’est le mot français pour… « fish ». Prononcez « pwa-sahn », avec le « oi » comme « wah » et le « n » nasal à la fin. C’est un mot masculin, en français, « le poisson ».
Et le mot « poisson » en français, c’est aussi plein d’expressions :
- Gros poisson : « Groh pwah-sonn », ça veut dire un grand poisson, littéralement. Mais en expression, ça désigne une personne importante, influente. Le « big fish » du coin, en quelque sorte.
- Poisson rouge : Le classique poisson rouge, l’animal de compagnie doré.
- Petit poisson : L’inverse du gros poisson, évidemment.
- Les poissons : « Lè pwah-sohn », tout simplement « les poissons ».
- Poisson bleu : « Blue fish », pour les amateurs de couleurs.
- Poisson d’avril : Ah, le fameux « Poisson d’avril » ! La blague du 1er avril. Rien à voir avec les statistiques, mais c’est toujours bon à savoir.
Alors, la prochaine fois que vous entendrez « distribution de Poisson », pensez au poisson, mais surtout pensez aux chiffres, aux événements, et à la puissance de cet outil statistique. C’est bien plus qu’un simple poisson d’avril statistique.
VII. Identifier une Distribution de Poisson : Les Indices Révélateurs
Comment savoir si on a affaire à une distribution de Poisson ? Quelques indices :
- k, un entier non négatif, représente le nombre d’événements dans un intervalle donné.
- L’occurrence d’un événement n’affecte pas la probabilité d’un autre événement. Indépendance, toujours.
- Le taux moyen d’événements est constant et indépendant des occurrences passées.
VIII. L’Approximation de Poisson : Quand Poisson Vient à la Rescousse
L’approximation de Poisson, c’est quand on utilise la distribution de Poisson pour simplifier les calculs dans d’autres situations. En général, si la probabilité de succès (p) est inférieure ou égale à 0.1 et que le nombre d’essais (n) est supérieur ou égal à 40, on peut utiliser l’approximation de Poisson en pratique. C’est un raccourci utile dans certains cas.
IX. Autres Concepts : Poisson à Toutes les Sauces
Le nom « Poisson » se retrouve dans d’autres concepts, parfois plus avancés :
- Crochets de Poisson : Un outil mathématique utilisé en mécanique hamiltonienne, pour étudier les constantes du mouvement et les observables mesurables simultanément. Rien à voir avec les poissons, mais le nom est là.
- Expérience de Poisson : Un type d’expérience statistique qui classe les résultats en deux catégories, succès ou échec. Là encore, le lien avec la distribution de Poisson est plus indirect.
Voilà, on a fait le tour du « poisson statistique ». J’espère que cette exploration vous a éclairé, et que vous ne confondrez plus jamais distribution de Poisson et poisson pané. Bonne pêche statistique !