Décortiquons le « P » : Plus qu’une simple lettre, un monde de probabilités et bien plus encore !
Vous êtes-vous déjà demandé ce que signifiait réellement ce « P » omniprésent dans les équations et les formules ? Non, pas le « P » de « prix » sur l’étiquette de vos croissants (quoique, la probabilité de trouver un bon croissant à Paris est un sujet statistique en soi !). Nous parlons du « P » qui se faufile dans les probabilités, la physique, et même la biologie. Accrochez-vous, car on va explorer les multiples visages de cette lettre mystérieuse, en commençant par un domaine où elle règne en maître : la distribution de Poisson.
1. La Distribution de Poisson : L’art de compter l’inattendu
Définition et Formule : Quand l’aléatoire devient prévisible (presque)
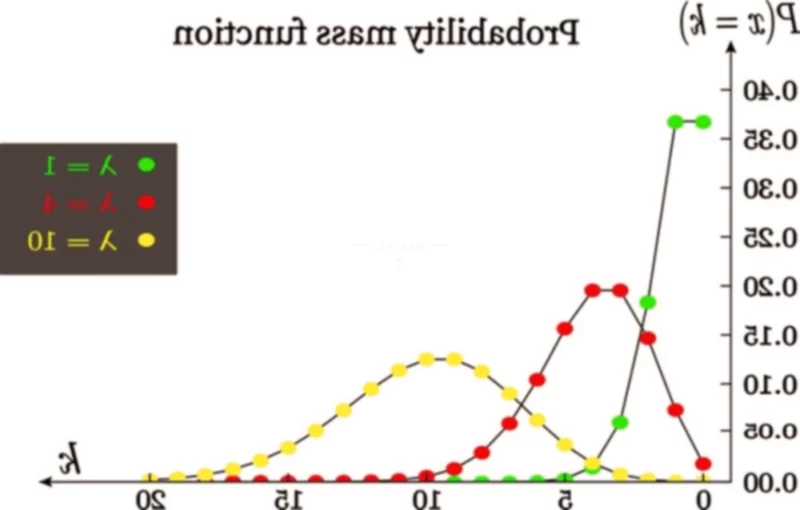
Imaginez : vous attendez le bus, et vous vous demandez combien vont arriver dans les 15 prochaines minutes. Ou peut-être, vous êtes chef cuisinier et vous voulez anticiper le nombre de clients qui vont commander votre fameuse soupe à l’oignon entre midi et 13h. La distribution de Poisson est là pour vous aider ! Elle calcule la probabilité d’un certain nombre d’événements se produisant dans un intervalle de temps ou d’espace donné, à condition que ces événements soient indépendants et se produisent à un rythme constant. C’est un peu comme essayer de prévoir les caprices de la météo, mais en plus précis et… mathématique.
La formule magique, la voici : f(x) = P(X=x) = (e – λ λ x )/x! Un peu effrayant au premier abord, mais décortiquons-la ensemble :
- f(x) ou P(X=x) : C’est la probabilité que l’on cherche à calculer. La probabilité d’observer exactement « x » succès.
- e : Un nombre mathématique un peu spécial, environ 2.71828. On l’appelle la base du logarithme naturel. Ne vous inquiétez pas, vous n’avez pas besoin de le calculer à la main !
- λ (lambda) : La star de la formule ! C’est la moyenne du nombre de succès attendus dans un intervalle donné. Par exemple, si en moyenne 5 clients commandent de la soupe à l’oignon par heure, λ = 5.
- x : Le nombre de succès pour lequel on veut calculer la probabilité. Si vous voulez savoir quelle est la probabilité que 3 clients commandent de la soupe à l’oignon, alors x = 3.
- x! (factorielle de x) : C’est le produit de tous les nombres entiers positifs jusqu’à x. Par exemple, 3! = 3 * 2 * 1 = 6.
En bref, cette formule, c’est la clé pour déchiffrer les mystères des événements aléatoires qui se produisent à un rythme régulier. Envie d’en savoir plus ? Ce lien vers Byjus vous donnera encore plus de détails sur la distribution de Poisson.
Paramètres : Un seul ingrédient secret, lambda (λ)
Contrairement à certaines distributions statistiques plus complexes, la distribution de Poisson est plutôt simple. Elle n’a besoin que d’un seul paramètre : lambda (λ). Ce lambda, c’est la moyenne du nombre d’événements dans un intervalle donné. Certains bouquins de statistiques l’appellent θ (thêta), mais ne vous laissez pas embrouiller, c’est le même ingrédient secret. Et une chose importante à retenir : lambda doit toujours être positif (λ > 0). C’est logique, on ne peut pas avoir une moyenne d’événements négative, à moins de compter des événements inexistants, ce qui serait un concept philosophique fascinant, mais hors sujet ici.
La beauté de lambda, c’est qu’il est à la fois la moyenne E(X) = λ et la variance de la distribution de Poisson. Variance ? C’est une mesure de la dispersion des données autour de la moyenne. Dans le cas de Poisson, la dispersion est directement liée à la moyenne. Élégant, non ?
Caractéristiques et Conditions : Quand Poisson entre en jeu
La distribution de Poisson n’est pas une baguette magique universelle. Elle fonctionne sous certaines conditions, un peu comme une recette de cuisine a besoin d’ingrédients spécifiques. Voici les conditions clés pour pouvoir utiliser Poisson :
- Indépendance des événements : Un événement qui se produit n’influence pas la probabilité qu’un autre événement se produise. L’arrivée d’un client pour la soupe n’empêche pas l’arrivée d’un autre.
- Événements discrets : On compte des événements, pas des mesures continues. Nombre de voitures qui passent, nombre d’erreurs d’impression, nombre de défauts dans un tissu… On parle de chiffres entiers, pas de 2,5 voitures ou 3,7 défauts.
- Taux moyen constant : Le taux moyen d’événements (lambda) reste constant pendant la période étudiée. Si le taux de clients qui commandent de la soupe change radicalement entre midi et 13h, Poisson pourrait ne plus être adapté.
- Événements rares : Bien que ce ne soit pas une condition absolue, la distribution de Poisson fonctionne particulièrement bien lorsque la probabilité d’un événement individuel est faible, mais que le nombre d’opportunités pour que cet événement se produise est élevé. Pensez aux appels téléphoniques à un standard, aux pannes d’une machine, aux erreurs de frappe dans un livre…
En résumé, Poisson est idéal pour compter des événements rares et indépendants qui se produisent à un rythme constant. C’est un outil puissant pour analyser des phénomènes variés, des files d’attente aux défauts de fabrication.
Moyenne et Variance : Les jumeaux de Poisson
On l’a déjà mentionné, mais c’est tellement important qu’on le répète : pour une distribution de Poisson, la moyenne et la variance sont égales. **E(X) = V(X) = λ**. C’est une caractéristique unique et très pratique. Si vous connaissez la moyenne, vous connaissez automatiquement la variance, et vice versa. C’est comme avoir deux informations pour le prix d’une !
Applications : Poisson à la rescousse !
Où utilise-t-on concrètement la distribution de Poisson ? Partout où l’on a besoin de modéliser des événements rares et aléatoires !
- Files d’attente (ou modèles d’attente) : Combien de guichets ouvrir dans une banque ? Combien de serveurs prévoir dans un restaurant ? Poisson aide à optimiser les ressources en prévoyant le nombre de clients ou d’appels entrants.
- Contrôle qualité : Combien de défauts peut-on s’attendre à trouver dans un lot de production ? Poisson permet de définir des seuils d’acceptabilité et de surveiller la qualité.
- Biologie : Nombre de mutations génétiques par génération, répartition des animaux dans un habitat, nombre de bactéries dans un échantillon… Poisson est un outil précieux en écologie et en génétique.
- Assurance : Nombre de sinistres par an, nombre d’accidents de voiture… Poisson aide à évaluer les risques et à calculer les primes.
- Télécommunications : Nombre d’appels téléphoniques par heure, nombre d’erreurs de transmission… Poisson permet de dimensionner les réseaux et d’améliorer la qualité de service.
Et la liste est encore longue ! La distribution de Poisson est une véritable boîte à outils pour tous ceux qui travaillent avec des données de comptage.
Concepts Associés : Dans la famille Poisson
La distribution de Poisson n’est pas un électron libre dans le monde des statistiques. Elle est liée à d’autres concepts importants :
- Processus de Poisson : C’est le cadre théorique général qui décrit l’occurrence d’événements aléatoires et indépendants dans le temps ou l’espace. La distribution de Poisson est en quelque sorte une « tranche » du processus de Poisson, en se concentrant sur le nombre d’événements dans un intervalle fixe.
- Distribution de Poisson tronquée à zéro (ZTP) : Imaginez que vous comptez le nombre de clients qui commandent de la soupe à l’oignon, mais vous ne pouvez observer que les jours où il y a au moins une commande. La distribution ZTP est une version modifiée de Poisson qui exclut la possibilité d’avoir zéro événement. Wikipedia vous en dit plus si vous êtes curieux.
Calculs : Poisson en pratique
Comment calcule-t-on concrètement une probabilité avec la formule de Poisson ? Rien de sorcier ! Il suffit de connaître lambda (la moyenne) et x (le nombre d’événements souhaité) et de brancher ces valeurs dans la formule : P(X=x) = (e – λ λ x )/x!
Par exemple, si en moyenne 2 erreurs d’impression se produisent par page d’un livre (λ = 2), et que vous voulez calculer la probabilité d’avoir exactement 3 erreurs sur une page (x = 3), vous appliquez la formule :
P(X=3) = (e – 2 2 3 )/3! ≈ 0.1804
La probabilité d’avoir exactement 3 erreurs sur une page est d’environ 18%. Des calculatrices en ligne ou des logiciels statistiques peuvent vous faciliter la vie pour ces calculs. Mais le principe reste simple : lambda, x, et hop, Poisson fait le reste.
Approximations : Quand Poisson se prend pour une autre
Dans certaines situations, la distribution de Poisson peut servir d’approximation à d’autres distributions, notamment la distribution binomiale et la distribution normale.
- Approximation de la binomiale par Poisson : La distribution binomiale décrit le nombre de succès lors d’un nombre fixe d’essais indépendants. Si le nombre d’essais (n) est très grand et la probabilité de succès (p) est très faible, la distribution de Poisson avec λ = n*p devient une bonne approximation de la binomiale. En pratique, on utilise souvent cette approximation quand n > 50 et np < 5, ou encore quand p ≤ 0.1 et n ≥ 40.
- Approximation de la Poisson par la normale : Pour des valeurs de lambda suffisamment grandes (disons, λ ≥ 10), la distribution de Poisson commence à ressembler à une distribution normale. C’est une conséquence du théorème central limite. On peut alors approximer une distribution Poisson(λ) par une distribution normale de moyenne μ = λ et d’écart-type σ = √λ. Par exemple, une distribution Poisson(100) peut être approximée par une distribution normale N(100, 10).
Ces approximations sont utiles pour simplifier les calculs ou pour utiliser des outils statistiques conçus pour la distribution normale.
Distributions Associées : Familles statistiques
On a déjà évoqué la distribution binomiale et la distribution normale. Comparons-les un peu plus avec la distribution de Poisson :
- Binomiale vs. Poisson : La distribution binomiale est adaptée quand on a un nombre fixe d’essais (n) et une probabilité de succès constante (p) pour chaque essai. Poisson, elle, est plus appropriée quand on a un nombre variable d’essais et un taux moyen d’événements constant. En gros, binomiale : nombre d’essais fixe, Poisson : intervalle de temps ou d’espace fixe.
- Normale vs. Poisson : La distribution normale est symétrique, en forme de cloche. La distribution de Poisson, elle, est généralement asymétrique, surtout pour les petites valeurs de lambda. Plus lambda augmente, plus Poisson se rapproche de la symétrie de la normale. Autre différence : la normale est continue (elle peut prendre n’importe quelle valeur réelle), Poisson est discrète (elle ne prend que des valeurs entières positives).
P-valeur dans la Distribution de Poisson : Tester l’hypothèse
Le fameux p-value ! Dans le contexte de la distribution de Poisson, la p-valeur sert à tester une hypothèse statistique. Elle représente la probabilité d’obtenir un résultat au moins aussi extrême que celui observé dans nos données, si l’hypothèse nulle (l’hypothèse que l’on cherche à réfuter) est vraie et que les données suivent bien une distribution de Poisson. Une p-valeur faible (généralement inférieure à 0.05) suggère que l’hypothèse nulle est peu probable et qu’il y a un effet statistiquement significatif.
Régression de Poisson : Modéliser les données de comptage
La régression de Poisson est une technique statistique utilisée pour modéliser des données de comptage, c’est-à-dire des variables qui représentent des nombres d’événements. Par exemple, le nombre de visites aux urgences par mois, le nombre de crimes par quartier, le nombre de produits défectueux par lot… L’idée de base est de supposer que la variable de réponse suit une distribution de Poisson et que le logarithme de sa valeur moyenne peut être modélisé par une combinaison linéaire de variables explicatives. C’est un outil puissant pour analyser les facteurs qui influencent les données de comptage.
Le Crochet de Poisson de P et Q : Physique théorique au menu
On s’éloigne un peu des probabilités pures pour explorer un concept de physique théorique : le crochet de Poisson. Dans la mécanique hamiltonienne, le crochet de Poisson est une opération qui associe deux fonctions de l’espace des phases (positions et moments) et qui mesure en quelque sorte leur « non-commutativité ». Pour les variables de base de la mécanique classique (positions q et moments p), les crochets de Poisson ont des propriétés bien définies :
- [qi, qk] = 0
- [pi, pk] = 0
- [pi, qk] = δik (delta de Kronecker, qui vaut 1 si i=k et 0 sinon)
Et plus généralement, le crochet de Poisson du moment p avec une fonction f(q) des positions est donné par : [p, f(q)] = df/dq. Ces crochets de Poisson sont fondamentaux en mécanique hamiltonienne et sont liés aux symétries et aux quantités conservées d’un système physique. Envie d’explorer ce monde fascinant ? Ce lien vers Galileo et Einstein vous ouvre les portes des crochets de Poisson.
Équation de Poisson : L’électricité statique dévoilée
Retour à la physique, mais cette fois-ci à l’électrostatique. L’équation de Poisson est une équation aux dérivées partielles qui relie le potentiel électrique à la distribution de charges électriques. Elle s’écrit généralement sous la forme : ∇2Φ = -ρ/ε0 où ∇2 est le laplacien, Φ est le potentiel électrique, ρ est la densité de charge, et ε0 est la permittivité du vide. Dans le Système International, l’équation se simplifie souvent en ∇2Φ = σ(x), où σ(x) est un terme source qui représente la distribution de charges. Si l’espace est vide de charges, l’équation de Poisson se réduit à l’équation de Laplace : ∇2Φ = 0. L’équation de Poisson est un outil essentiel pour résoudre des problèmes d’électrostatique et pour calculer le potentiel électrique créé par une distribution de charges donnée.
2. Le « P » sous toutes ses coutures : Un alphabet statistique et scientifique
On a vu le « P » de Poisson, mais il se cache dans bien d’autres recoins des sciences. Décryptons quelques-unes de ses autres significations.
Probabilité Générale : P comme « Possible »
Le « P » le plus fondamental, c’est celui de la probabilité en général. **P(A)** désigne la probabilité d’un événement A. Par exemple, si A est l’événement « obtenir pile en lançant une pièce », P(A) = 0.5 (si la pièce est équilibrée). La probabilité est toujours un nombre entre 0 et 1, où 0 signifie « impossible » et 1 signifie « certain ». La formule de base de la probabilité est :
**P(A) = n(A) / n(S)**
Où n(A) est le nombre de résultats favorables à l’événement A, et n(S) est le nombre total de résultats possibles (l’espace échantillonnal S). Simple, efficace, et fondamental.
Équation de Hardy-Weinberg : P pour les allèles dominants
En génétique des populations, l’équation de Hardy-Weinberg décrit l’équilibre des fréquences alléliques et génotypiques dans une population qui n’évolue pas. Dans cette équation, « p » représente la fréquence de l’allèle dominant, et « q » la fréquence de l’allèle récessif. Et la relation fondamentale : **p + q = 1**. Ce « p » est donc crucial pour comprendre la génétique des populations et l’évolution.
Distribution Binomiale : P pour la probabilité de succès
On a déjà croisé la distribution binomiale. Dans ce contexte, « p » désigne la probabilité de succès lors d’un seul essai. Par exemple, si on lance un dé à six faces et qu’on considère un succès comme « obtenir un 6 », alors p = 1/6. Ce « p » est un paramètre essentiel de la distribution binomiale, avec le nombre d’essais « n ».
Probabilité Statistique : P comme « Pertinence »
En statistiques, le « P » peut aussi désigner la p-valeur, dont on a déjà parlé pour la distribution de Poisson. Plus généralement, en statistiques inférentielles, le « P » peut représenter une probabilité associée à un test statistique. Il mesure la probabilité que la différence observée entre des groupes soit due au hasard seul. Un « P » faible suggère que la différence est statistiquement significative.
Valeur P (p-value) : P pour « Probabilité de l’hypothèse nulle »
La p-valeur, ou « probability value » en anglais, est un concept central des tests d’hypothèses. Elle quantifie la probabilité d’obtenir des données aussi extrêmes (ou plus extrêmes) que celles observées, si l’hypothèse nulle est vraie. Encore une fois, une p-valeur faible (typiquement < 0.05) remet en question l’hypothèse nulle.
Croissance de Population : P pour « Population Finale »
Dans les modèles de croissance de population, « P » peut représenter la taille de la population finale, après une certaine période de temps. C’est un « P » de résultat, qui dépend des paramètres du modèle de croissance (taux de natalité, taux de mortalité, etc.).
Intérêts Composés : P pour « Principal »
Dans le monde des finances, et plus précisément des intérêts composés, « P » désigne le capital initial, ou principal. C’est la somme de départ qui va fructifier avec le temps grâce aux intérêts. Un « P » qui, on l’espère, grandira avec les années !
Physique : P pour Puissance, Pression, et Momentum
La physique est un terrain de jeu fertile pour le « P » :
- Puissance électrique : P = VI (tension * courant) ou P = I2R (carré du courant * résistance). Le « P » de la puissance électrique, mesurée en watts.
- Pression : P = F/A (force / aire). Le « P » de la pression, mesurée en pascals.
- Momentum (quantité de mouvement) : Le momentum d’une particule est conventionnellement représenté par la lettre « p » (minuscule cette fois !). Une confusion possible avec la probabilité « P » (majuscule), mais le contexte aide généralement à distinguer.
Équation de la Courbe de Demande : P pour Prix
En économie, dans l’équation de la courbe de demande linéaire P = a – bQ, « P » représente le prix. « Q » est la quantité demandée, « a » est l’ordonnée à l’origine, et « b » est la pente de la courbe de demande. Un « P » crucial pour comprendre les mécanismes du marché.
3. Probabilité et P-valeur : Un couple infernal (au bon sens du terme)
On a déjà croisé la p-valeur à plusieurs reprises. Faisons le point sur sa relation avec la probabilité générale.
P-valeur : Probabilité sous condition
La p-valeur est une probabilité, mais pas n’importe laquelle. C’est la probabilité d’observer des données aussi extrêmes (ou plus extrêmes) que celles que l’on a, en supposant que l’hypothèse nulle est vraie. C’est donc une probabilité conditionnelle. Comme toute probabilité, la p-valeur est comprise entre 0 et 1. Une p-valeur proche de 0 indique que les données observées sont très peu probables si l’hypothèse nulle est vraie, ce qui remet en question cette hypothèse. Inversement, une p-valeur proche de 1 suggère que les données observées sont compatibles avec l’hypothèse nulle.
Un seuil de p-valeur couramment utilisé est 0.05. Si la p-valeur est inférieure à 0.05, on rejette généralement l’hypothèse nulle au seuil de 5%. Cela correspond à un intervalle de confiance à 95%. Attention, cela ne signifie pas qu’il y a 5% de chances que l’hypothèse nulle soit vraie, mais plutôt qu’il y a 5% de chances d’observer des données aussi extrêmes que celles observées si l’hypothèse nulle était vraie.
Probabilité : La base de tout
La probabilité, au sens général, est la mesure de la possibilité qu’un événement se produise. Elle est définie comme le rapport entre le nombre de cas favorables et le nombre de cas possibles. C’est un concept fondamental qui sous-tend de nombreux domaines, des statistiques aux jeux de hasard, en passant par la physique quantique. Et, bien sûr, la p-valeur est elle-même une forme de probabilité, mais une probabilité bien spécifique, conditionnée à l’hypothèse nulle.
4. Poisson face aux autres : Duel de distributions
On a déjà comparé Poisson à la binomiale et à la normale. Récapitulons ces différences et similitudes.
Poisson vs. Binomiale : Le match des comptages
Le choix entre Poisson et la binomiale dépend du contexte. Si vous avez un nombre fixe d’essais (n) et une probabilité de succès constante (p), la binomiale est la distribution appropriée. Si vous avez un intervalle de temps ou d’espace fixe et un taux moyen d’événements constant, Poisson est plus adaptée. En résumé :
- Binomiale : Nombre d’essais fixe, probabilité de succès fixe. Exemple : nombre de faces « pile » en 10 lancers de pièce.
- Poisson : Intervalle fixe, taux moyen fixe. Exemple : nombre de voitures qui passent à un péage en 1 heure.
Et on l’a vu, dans certaines conditions (n grand, p petit), Poisson peut approximer la binomiale.
Poisson vs. Normale : Formes et symétries
La distribution normale est toujours symétrique, en forme de cloche. La distribution de Poisson, elle, est généralement asymétrique, surtout pour les petites valeurs de lambda. Plus lambda augmente, plus Poisson tend vers la symétrie de la normale. C’est pourquoi, pour les grandes valeurs de lambda, on peut approximer Poisson par une normale. Mais pour les petites valeurs de lambda, Poisson conserve sa forme asymétrique caractéristique.
5. Ratio de Poisson : Déformation sous pression
On change de domaine et on explore le ratio de Poisson, un concept de mécanique des matériaux.
Définition du Ratio de Poisson : L’effet « ventouse »
Le ratio de Poisson décrit comment un matériau se déforme transversalement lorsqu’il est soumis à une contrainte axiale (traction ou compression). Imaginez que vous étirez un élastique : il s’allonge dans le sens de la traction, mais il se rétrécit aussi latéralement. Le ratio de Poisson quantifie ce rétrécissement latéral par rapport à l’allongement axial. Plus précisément, c’est la valeur négative du rapport entre la déformation transversale et la déformation axiale. Pourquoi négative ? Parce que généralement, quand un matériau s’allonge axialement (déformation axiale positive), il se rétrécit transversalement (déformation transversale négative), et vice versa. Le ratio de Poisson est donc souvent positif pour les matériaux courants.
Formule du Ratio de Poisson : Nu, la lettre grecque
Le ratio de Poisson est symbolisé par la lettre grecque « nu » (ν). Sa formule est :
**ν = – Déformation latérale / Déformation longitudinale**
Les déformations sont des variations de longueur relatives à la longueur initiale. Le ratio de Poisson est une grandeur sans dimension, typiquement comprise entre 0 et 0.5 pour les matériaux courants.
Ratio de Poisson Négatif : L’exception qui confirme la règle
La plupart des matériaux ont un ratio de Poisson positif, mais il existe des matériaux avec un ratio de Poisson négatif ! Ces matériaux, dits « auxétiques », ont la particularité de se dilater transversalement lorsqu’ils sont étirés axialement, et de se contracter transversalement lorsqu’ils sont comprimés axialement. Un comportement contre-intuitif qui leur confère des propriétés intéressantes, par exemple en termes d’absorption d’énergie ou de confort. Les mousses auxétiques, certains polymères, et même certains cristaux présentent un ratio de Poisson négatif.
6. « P » en force : Momentum, l’élan invisible
En mécanique classique, le « p » minuscule désigne le momentum, ou quantité de mouvement, d’une particule. C’est une grandeur vectorielle qui mesure l’inertie d’un corps en mouvement. Pour une particule de masse « m » et de vitesse « v », le momentum est donné par :
**p = mv**
Le momentum se conserve dans un système isolé, c’est-à-dire en l’absence de forces extérieures. C’est un principe fondamental de la physique, qui explique par exemple le recul d’un canon ou la propulsion d’une fusée.
7. P-valeur en directrice : Géométrie des paraboles
En géométrie analytique, et notamment dans l’étude des paraboles, la « p-valeur » intervient dans la définition du foyer et de la directrice. Pour une parabole d’équation canonique y2 = 4px (ou x2 = 4py), la distance entre le sommet et le foyer (et aussi la distance entre le sommet et la directrice) est égale à « p ». La directrice est une droite perpendiculaire à l’axe de symétrie de la parabole, située à une distance « p » du sommet, de l’autre côté du foyer. La p-valeur est donc un paramètre géométrique important pour caractériser une parabole.
8. « P » différentiel : Les globules blancs à la loupe
Dans le domaine médical, le « P » peut aussi intervenir dans l’expression « formule leucocytaire » ou « différentiel leucocytaire ». Cette formule, obtenue par un examen sanguin, donne les pourcentages des différents types de globules blancs (leucocytes) présents dans le sang : neutrophiles, lymphocytes, monocytes, éosinophiles, basophiles. Le « P » du « différentiel » n’a pas de signification mathématique particulière, c’est juste une abréviation pour « pourcentage » ou « proportion ». L’analyse de la formule leucocytaire est un outil diagnostique important pour détecter des infections, des inflammations, ou des maladies hématologiques.
9. Équation de Poisson de la pression : Fluides en mouvement
On termine notre exploration du « P » avec l’équation de Poisson de la pression, un concept de mécanique des fluides. Cette équation est dérivée des équations de Navier-Stokes, qui décrivent le mouvement des fluides visqueux. Pour un fluide incompressible, l’équation de Poisson de la pression relie le gradient de pression au champ de vitesse du fluide :
∇2p = -ρ ∇ · (u · ∇)u
Où p est la pression, ρ est la masse volumique du fluide, et u est le champ de vitesse. Cette équation est utilisée pour résoudre des problèmes d’écoulement de fluides et pour calculer la distribution de pression dans un fluide en mouvement. Elle est particulièrement utile en turbulence, où les fluctuations de pression jouent un rôle important.
Voilà, notre voyage à travers les multiples significations du « P » s’achève. De la probabilité aux statistiques, en passant par la physique, la génétique, la finance, la géométrie, la médecine, et la mécanique des fluides, le « P » est une lettre caméléon qui s’adapte à tous les contextes. Espérons que cette exploration vous aura éclairé sur les visages cachés de ce « P » omniprésent, et que vous ne le regarderez plus jamais de la même manière !