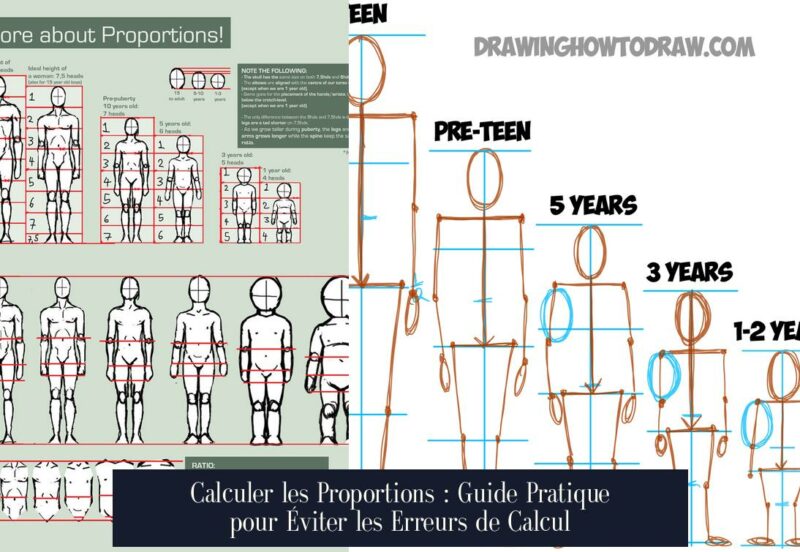
Comment calculer les proportions ? Le guide hilarant pour ne plus jamais être à côté de la plaque !
Vous vous êtes déjà retrouvé face à une recette en vous demandant comment diable ajuster les quantités pour 10 personnes alors qu’elle est prévue pour 4 ? Ou peut-être avez-vous contemplé un plan de maison en vous demandant si votre canapé rentrerait vraiment dans ce salon miniature ? Pas de panique ! Calculer les proportions, c’est un peu comme maîtriser l’art de la magie… sans baguette, mais avec des chiffres.
Calculer les proportions, c’est avant tout une question de logique et de bon sens, un peu comme trouver la chaussette orpheline dans votre tiroir, mais en plus simple (promis !). En réalité, c’est une compétence super pratique dans la vie de tous les jours, que ce soit en cuisine, en bricolage, ou même pour comprendre les statistiques (oui, oui, même ça !).
Alors, comment on fait concrètement ? Accrochez-vous, on déchiffre tout ça ensemble, avec une pincée d’humour pour que ça glisse tout seul, comme une crêpe au Nutella un dimanche matin.
Les bases, les fondations, le B.A.-BA des proportions (en mode facile)
Imaginez une recette de gâteau au chocolat (miam !). Elle indique 2 œufs pour 6 personnes. Mais voilà, vous avez une armée de gourmands qui débarquent, soit 12 personnes. Logiquement, il va falloir doubler les quantités, non ? Bingo ! C’est ça, la proportionnalité. On multiplie tous les ingrédients par 2 pour garder le même équilibre, le même ratio, la même magie gustative.
En mathématiques, une proportion, c’est une égalité entre deux rapports. Un rapport, c’est simplement une fraction, une division. Par exemple, si 2 œufs correspondent à 6 personnes, le rapport est 2/6. Pour 12 personnes, on cherche un rapport équivalent, du type x/12, où ‘x’ est le nombre d’œufs qu’il nous faut.
Pour trouver ‘x’, on utilise la fameuse règle de trois, ou produit en croix, appelez ça comme vous voulez, l’important c’est que ça marche !
La règle de trois, votre alliée proportionnelle (et pas que pour le gâteau)
La règle de trois, c’est un peu la baguette magique des proportions. Elle se présente comme ça :
Si a/b = c/d alors a x d = b x c
Reprenons notre exemple des œufs et des gourmands :
2 œufs / 6 personnes = x œufs / 12 personnes
On applique la règle de trois :
2 œufs x 12 personnes = 6 personnes x x œufs
24 = 6x
Pour trouver ‘x’, on divise 24 par 6 :
x = 24 / 6 = 4
Et voilà ! Il vous faudra 4 œufs pour votre gâteau au chocolat pour 12 personnes. Facile, non ? Presque aussi facile que de résister à une part de ce gâteau… presque.
Exemples concrets et rigolos pour apprivoiser les proportions
- Le plan de maison et votre canapé géant : Si sur le plan, 1 cm représente 1 mètre en réalité (l’échelle est de 1:100), et que votre salon mesure 5 cm sur le plan, alors en réalité, il fera 5 mètres de long. Si votre canapé fait 3 mètres de long, il rentrera (ouf !). Les proportions vous évitent de vous retrouver avec un canapé qui bloque la porte d’entrée.
- Le dosage de peinture pour repeindre votre salon en jaune soleil : Si le pot de peinture indique qu’il couvre 10 m2 et que votre salon fait 20 m2, il vous faudra logiquement deux pots de peinture (sauf si vous voulez un effet artistique « inachevé », mais c’est un autre débat). Les proportions, c’est aussi éviter de se retrouver à court de peinture au milieu du chantier, avec un mur à moitié jaune et l’autre blanc. Le drame.
- Les soldes et les pourcentages de réduction : Si un article à 100€ est soldé à -30%, la réduction est de (30/100) x 100€ = 30€. Le prix soldé sera donc de 100€ – 30€ = 70€. Comprendre les proportions, c’est aussi éviter de se faire arnaquer par des « promotions » qui n’en sont pas vraiment. L’arnaque, non merci !
Petits pièges à éviter et astuces de pro (enfin, presque)
- Attention aux unités ! Si vous mélangez des centimètres et des mètres, des grammes et des kilos, ça ne marchera pas. Mettez toujours toutes les mesures dans la même unité avant de faire vos calculs. C’est comme comparer des pommes et des oranges, ça n’a pas de sens.
- Simplifiez les rapports quand c’est possible. 2/6, c’est pareil que 1/3. Ça peut simplifier vos calculs et rendre les choses plus claires. Un peu comme ranger votre bureau avant de travailler, ça aide à y voir plus clair.
- N’hésitez pas à utiliser une calculatrice. Surtout pour les calculs complexes ou avec des grands nombres. La calculatrice, c’est votre amie, elle ne vous jugera pas si vous avez du mal avec les multiplications à virgule.
Pour aller plus loin (si le cœur vous en dit)
Si vous avez vraiment envie de devenir un maître des proportions (et impressionner vos amis lors de votre prochain dîner), vous pouvez explorer les notions de proportionnalité directe et proportionnalité inverse. Mais pour le quotidien, la règle de trois et un peu de logique suffisent largement.
Et si vous voulez une explication encore plus visuelle et dynamique, n’hésitez pas à jeter un œil à cette vidéo d’Alloprof sur YouTube : Les proportions | Mathématiques | Alloprof – YouTube. Ils sont super pédagogues et rendent les maths presque amusantes (si, si, c’est possible !).
Source : Les proportions | Mathématiques | Alloprof – YouTube
Conclusion : Les proportions, c’est dans la poche (et dans le gâteau) !
Voilà, vous savez maintenant comment calculer les proportions. Ce n’est pas sorcier, n’est-ce pas ? Avec un peu de logique, la règle de trois et quelques exemples rigolos, les proportions n’auront plus de secrets pour vous. Vous pourrez enfin adapter vos recettes, décrypter les plans de maison et même comprendre les soldes (le Graal !). Alors, à vous de jouer, et n’oubliez pas, les maths, c’est comme le vélo, ça s’apprend… et après, on ne peut plus s’en passer ! Et si vous avez encore des doutes, relisez cet article, regardez la vidéo d’Alloprof, ou demandez à votre voisin matheux (il en existe sûrement un, caché quelque part). Les proportions, c’est à la portée de tous, promis juré craché !